May 6th, 2024
Deciphering Preferences with the Sign Test
By Josephine Santos · 7 min read

Overview
In the realm of statistical analysis, the Sign test stands out as a non-parametric method used to determine if two groups are equally sized. This test is particularly useful when dealing with dependent samples ordered in pairs and is based on the direction of the plus and minus signs of the observation, rather than their numerical magnitude. It's also known as the binomial sign test, with a probability (p) of 0.5. Despite being considered a weaker test because it doesn't measure the pair difference, the Sign test is a valuable tool in certain scenarios.
Understanding the Sign Test
Assumptions of the Sign Test
2. Two Sample: The data should come from two samples, which may differ.
3. Dependent Sample: The samples should be paired or matched, also known as ‘before-after’ samples.
Types of Sign Test
2. Paired Sample: Also an alternative to the paired t-test, this test uses the + and – signs in paired sample tests or in before-after studies.
Procedure of the Sign Test
1. Calculate the + and – signs for the given distribution. Put a + sign for a value greater than the mean value, and put a – sign for a value less than the mean value. Put 0 as the value is equal to the mean value; pairs with 0 as the mean value are considered ties.
2. Denote the total number of signs by ‘n’ and the number of less frequent signs by ‘S.’
3. Obtain the critical value (K) at a 0.05 significance level for small samples:
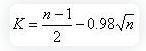
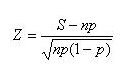

Implementing the Sign Test in SPSS
SPSS offers a straightforward way to conduct a Sign test:
1. Open the SPSS software and select your data.
2. Choose “nonparametric test” from the analysis menu, then “two related samples.”
3. Select your paired variables and choose the “sign test” from the available tests.
4. The result window will provide descriptive statistics, a frequency table, and test statistics for the Sign test.
Conclusion
The Sign test is a unique and valuable tool in the statistical arsenal, especially when dealing with non-parametric data. Its simplicity and focus on the direction of changes make it a go-to method for specific research questions. For those looking to delve deeper into data analysis and leverage the power of tools like SPSS, Julius can be an invaluable resource. With its ability to assist in data analysis and interpretation, Julius can help you unlock the full potential of the Sign test and other statistical methods, guiding you towards more accurate and insightful conclusions.
