July 21st, 2024
Guide to Descriptive Statistics: Definition, Types, and More
By Rahul Sonwalkar · 7 min read
Collecting. Organizing. Describing. Analyzing. Interpreting. These are the five most common steps in the statistical analysis process. Each step is crucial for the step that follows, as well as the overall success of the research.
The third step – describing the data – is where the characteristics of the data set are summarized using descriptive statistics. Fail to present and describe raw data accurately, and you’ll end up with inaccurate analysis and a misinterpretation of results.
With this in mind, let’s look into descriptive statistical analysis and the statistical methods it employs.
What Are Descriptive Statistics?
Descriptive statistics is a type of statistical analysis whose goal is to organize, summarize, and present data in a concise and easy-to-understand manner. It’s important to emphasize that descriptive statistics doesn’t go any further than that. It doesn’t make generalizations, inferences, or predictions. It only prepares the data set for further analysis (e.g., inferential statistics) by providing a snapshot of its key characteristics.
In that regard, summary statistics is arguably the most important aspect of descriptive statistics. However, the importance of data visualization also can’t be understated, as charts, graphs, and tables greatly aid in understanding the data and communicating it to others, especially the non-professionals.
Why Is Descriptive Statistics Important?
Descriptive statistics is important for two reasons.
One, it’s a crucial tool in and of itself, as it allows researchers and analysts to understand the characteristics of a data set virtually at a glance. This understanding is essential for making informed decisions, identifying patterns or trends, and communicating findings to stakeholders (or the general public).
Two, descriptive statistics serves as the foundation for further statistical analysis. One look at the key aspects of the data sets tells researchers exactly which data analysis techniques are appropriate for further research.
Understanding the 3 Types of Descriptive Statistics
Most experts agree that there are three primary types of descriptive statistics: distribution, central tendency, and variability.
Distribution
Distribution, often referred to as frequency distribution, summarizes the number of times a specific data point occurs in a data set. Most commonly, the frequency distribution is presented in a table or a chart, such as a histogram or a bar graph, while the value itself is rendered as a number or a percentage.
Besides quantifying data points that appear in a data set, distribution can also measure data points that fail to occur. For instance, descriptive analysis of a data set consisting of product ratings will show how customers rated a product on a scale of 1 to 5, as well as the number of customers who didn’t provide a rating.
Central Tendency
Central tendency measures where the center (or average) of the data set is. The goal is to uncover the typical or representative value in the data, which can then be used to make comparisons or draw conclusions.
There are three ways to calculate the measures of central tendency – the mean, median, and mode:
- The mean represents the average of all values in a data set. Calculating this average is simple. You just add up all the values and divide the sum by the total number of values.
- As for the median, it represents the middle value in a data set when all the values are arranged in ascending or descending order. In other words, it’s the precise center of the data set.
- And finally, the mode. This is nothing but the most frequently occurring value in a data set. Beware, though – not all data sets will have a single mode. Some will have multiple modes, while others won’t have any.
Variability
Variability, also known as spread, refers to the extent to which data points differ from each other and from the central tendency. In other words, it demonstrates how spread out data points are.
Variability has three main aspects – the range, standard deviation, and variance:
- The range shows how far apart the most extreme values of the data set are. You can calculate this numerical value by subtracting the data set’s lowest value from its highest value.
- As far as standard deviation goes, this aspect demonstrates how far each data set lies from the mean. For a data set to be reliable and meaningful, the standard deviation should be low.
- The final aspect – variance – provides a measure of the overall variability of the data set, i.e., its spread. Calculating this value is also simple. Just square the standard deviation.
Univariate vs. Bivariate Descriptive Statistics
As the names imply, the primary difference between these two types of descriptive statistics is the number of variables they analyze. Univariate descriptive statistics analyzes only one variable, while bivariate descriptive statistics tackles two.
However, this isn’t the only difference between them.
Univariate
Univariate analysis focuses on summarizing and understanding the distribution, central tendency, and variability of a single variable. This analysis doesn’t deal with any relationships or causes; it merely provides a comprehensive overview of one variable’s characteristics.
The patterns identified using this method are often visualized in the form of histograms, bar graphs, and box plots.
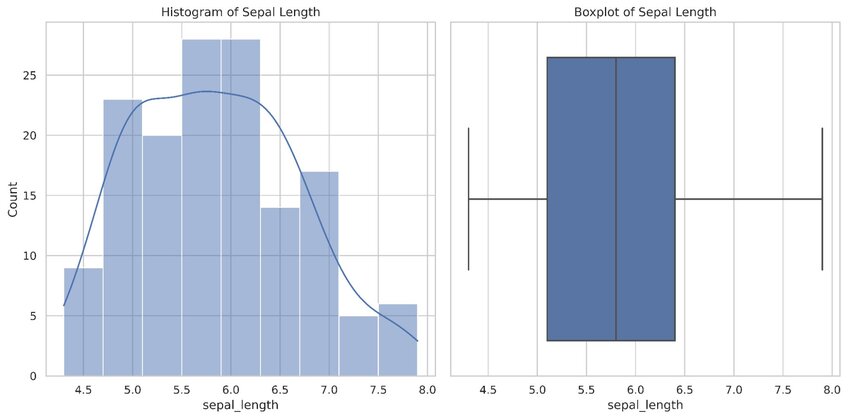
Univariate descriptive statistics example showing sepal length. Created in seconds with Julius AI
Bivariate
Bivariate analysis doesn’t only describe two variables. It also attempts to uncover whether they’re correlated. In this sense, the primary purpose of bivariate descriptive statistics isn’t describing, but explaining.
Bivariate and multivariate analysis methods are similar in this regard, but the latter method focuses on more than two variables at once. You’ll often see the findings of these methods visualized as scatter plots or cross-tabulations.
Example of Descriptive Statistics
Here’s a simple example of descriptive statistics techniques that should help you understand their practical application.
Imagine you teach a class of 11 students. Their scores on the last math quiz were as follows: 85, 92, 78, 90, 95, 88, 76, 85, 80, 82, and 91.
Now that you have your data set, here’s an overview of the descriptive statistics values you can calculate:
- The mean: 85 + 92 + 78 + 90 + 95 + 88 + 76 + 85 + 80 + 82 + 91 = 942 / 11 = 85.64
- The median: 85, as this is the number that appears in the middle of the data set when arranged in order.
- The mode: 85, as this is the only number that appears twice.
- The range: 95 - 76 = 19
How to Utilize Descriptive Statistics
As you can see from the example above, anyone can make descriptive statistics practical. You can use it to summarize and understand virtually any set of numerical data. If you aren’t particularly math savvy, you can use an AI-powered statistical analysis tool like Julius AI to do the calculations for you.
Make the Most of Statistical Analysis with Julius AI
The data sets you encounter in school, work, or everyday life will rarely have just 11 data points. So, calculating these values you need can quickly turn into a complex and time-consuming process. That is, if you do this without any help. If, however, you use Julius AI, you’ll need mere seconds to summarize any data set.
Give this incredible tool a try today to see for yourself.
